Introduction

Fluvial sediments accumulate at the coast and build river deltas, with multi-scale morphodynamics that are dynamically controlled by sediment availability, hydrodynamic conditions, and human activities1,2. Maintaining delta surface area is crucial for ecological services, socio-economic developments, resistance to storm surges, and coastal carbon burial3,4. However, fluvial sediment load delivery to many river deltas has been declining, triggered by varied natural and anthropogenic change (Supplementary Fig. 1)5,6,7, which has led to widespread concerns about the sustainability of delta surface area8,9,10,11.

To a first order, changes in delta surface area are linearly dependent on fluvial sediment supply and relative sea-level change, with \(\frac{d{A}_{{delta}}}{{dt}}\propto {Q}_{{river}}-{A}_{{delta}}{SLRR}\), where \({A}_{{delta}}\) is the delta land area (m2), t is a unit of time (yr), \({Q}_{{river}}\) is the fluvial sediment supply at the delta apex (m3 yr?1), and SLRR is the relative sea-level rise rate (m yr?1)12,13. Results of experimental and numerical simulations support this theory and show that the delta land area will grow at a constant rate under stable sea level, while the deltaic channel-edge length extends more rapidly14. A study analyzing surface area changes in deltas on a global scale also confirms that deltas that receive greater fluvial sediment supply generally grow faster11.

A logical, and practical, consequence of this relation is that deltas are expected to have altered rates of land area change in response to fluctuations in Qriver, i.e., \(\frac{{d}^{2}{A}_{{delta}}}{d{t}^{2}}\propto \,\frac{d{Q}_{{river}}}{{dt}}\), under a constant SLRR (Supplementary Fig. 2). For example, if a delta experiences a large decline in Qriver, their surface area growth rate will decline, even may lead to land loss over time if the fluvial sediment supply cannot keep up with the SLRR. However, despite the simplicity of this argument, there is only incidental evidence. For instance, after the mean suspended sediment concentration declined by over 70% during the past 200 years, tidal wetlands in the Mississippi River bird-foot delta retreated rapidly and at rates up to 9.0 km2 yr?1 between 1932 and 197113,15. In the Amazon Delta, benefiting from a 20% increase in upstream sediment input, coastal mangrove forests expanded overall by a net 157 km2 over the past four decades, accelerating from 1.3 km2 yr?1 in 1984–1999 to 6.0 km2 yr?1 in 2000–202116,17. However, studies that investigated river deltas along the Mediterranean Sea found no relation between land growth rates and fluvial sediment loads18. Even on a global scale, in a review of 50 deltas, there is mixed evidence, with a study concluding that declines in fluvial sediment supply have not, thus far, “had a significant negative impact on multi-decadal delta shoreline mobility”19. Recent work by Hou et al.20 found more surprises20. Many (45%) of the 349 deltaic coasts they studied had increasing sediment concentration under conditions of decreased fluvial sediment inputs between 2000 and 202020. This highlights one of the potentially many factors that affect delta land growth rate, complicating direct observations of the relation between fluvial sediment supply and delta surface area change.

Part of the complication in testing how fluctuations in fluvial sediment supply affect delta area is that there may be time lags. Deltas might take a long time to adjust to the changed external natural and anthropogenic drivers. Time lags appear in many places along Earth’s fluvial and deltaic sediment pathways21,22,23,24,25. They are well studied in river systems. For instance, a model study from Nittrouer and Viparelli (2014) showed that, through river channel slope adjustment, it may take centuries for the Mississippi sand supply to the delta to be affected by upstream dams26. Observations from the Elwha River (USA), where two large dams were removed in 2011-2014 that released significant amounts of trapped sediment, showed that the delta grew by 0.6 km2 within 5 years. The delta geomorphic response signal with a lag of 1–2 years was most significant27. In the S?o Francisco Delta (Brazil), coastal erosion that destroyed the Cabe?o village between 1997 and 1999 years after the construction of the Xingó Dam, which was completed in 1994. Dominguez & Guimar?es stressed that the time lag resulted from river regulation, which triggered coastal erosion through its influence on the deltaic backwater effect28.

Longer lag times were found in Japan, where dams were constructed before 1970, however, erosion rates only rose after 198029. Similarly, after the closure of the Hirakud Dam in 1956, annual fluvial sediment inputs were reduced by 67% in the wave-influenced Mahanadi Delta (India), and the delta retreat followed 20 years later30. These studies indicate that time lags within the drainage basin can vary and are in the order of years to centuries.

Studies of time lags within riverine deltas are rare. Evidence from the Yangtze Delta suggests that the delta area response can lag significantly behind dam construction. A relative increase in tidal dominance compared to river forcing can lead to landward movement of pro-delta sediments and, in effect, buffer the land area response and cause decadal time lags31,32. In contrast, in the Red River Delta (Vietnam), the shoreline retreat of the Ba Lat delta lobe only lagged approximately 1 year after the fluvial sediment reduction33. Even so, how these lags arise, and whether they are widespread in modern river deltas remains unclear. If time lags are present, and significant, it could explain why river delta response to fluvial sediment supply changes remains difficult to observe.

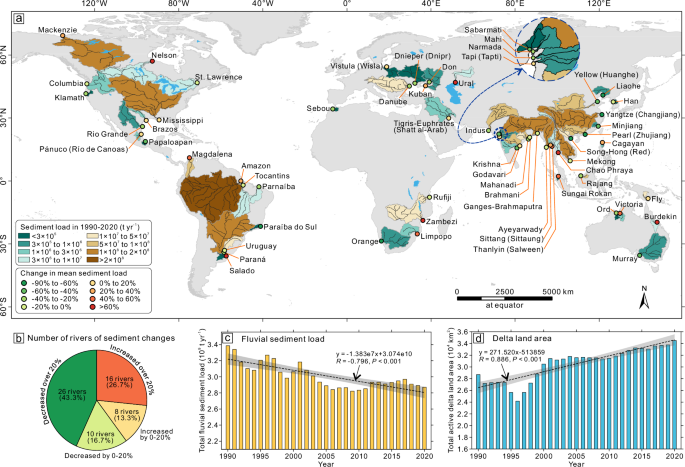
Here, we test the hypothesis that fluvial sediment supply change at the delta apex leads to a lagged response in the delta land area. We test this on a global scale for 60 deltas (Fig. 1a) and explore (1) the overall lag time between changes in delta area change rate and sediment supply between 1990 and 2020, and (2) the possible terrestrial and marine factors that affect lag times. Fluvial suspended sediment loads for these 60 deltas were obtained from Dethier et al.7 (see “Method”), using satellite-derived sediment fluxes from the delta apex. In addition, Landsat satellite imagery was used to compute delta land area changes for 60 studied deltas34. The definition of delta land and the drawing of polygons for individual deltas are shown in the Methods section (Fig. 2a and Supplementary Fig. 3).

Fig. 1: Global distribution of major river deltas and changes in fluvial sediment load and delta land area.
figure 1

a The location of the 60 studied major river deltas, shows the annual fluvial sediment loads entering the delta from the basins and the corresponding change proportions between 1990 and 2020. b Numbers of rivers with different proportions of sediment load variation. c, d Time series and linear fitting trends of annual total fluvial sediment load and active delta land area during the last 31 years.

Full size image
Fig. 2: Schematic illustration of delta land area changes and the cross-correlation analysis.
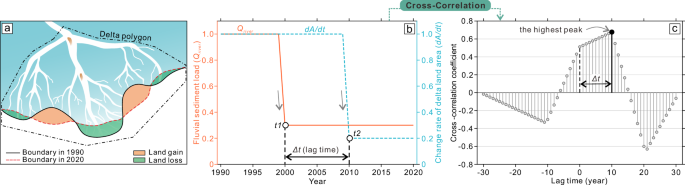
figure 2

a Schematized delta land gain and land loss. b A conceptual diagram showing the fluvial sediment load and delta land change rate with illustrated change at t1 and t2, respectively, and their lag time. c Calculated cross-correlation coefficients of different lag times and the primary lag time corresponded to the position of the highest correlation coefficient.

Full size image

We use the cross-correlation analysis to test our hypothesis (Fig. 2b, c). This is a method commonly used in the geosciences35,36,37 to examine the lagged behaviors between the two time series of variables (Fig. 2b). Specifically, when the fluvial sediment supply (Qriver) and delta land growth rate (dA/dt) changed at t1 and t2, respectively; the cross-correlation method first calculates the correlation coefficients of two lagged data of Qriver and dA/dt with different delayed time steps (years), then the primary lag time (?t) can be determined depending on the highest peak of the correlation coefficient (Fig. 2b, c).

By doing this analysis, we simplify the relationship between Qriver and dA/dt as being linear, which does not apply on longer (millennial) timescales because of increasing basin depths and increasing delta surface area11,38,39. We also assume that year-to-year changes in the SLRR are small compared to Qriver variability (Supplementary Table 1 and Supplementary Fig. 2)40,41. Further, because of the large diversity in governing hydrodynamics, geomorphology, and size of the 60 river deltas ultimately selected, we primarily analyze globally aggregated fluvial sediment load and land area in all deltas to test the overall lagged time, rather than first analyzing the lag times of 60 individual deltas and then averaging these results to achieve the delayed time. This method avoids, to a certain extent, the possible errors caused by biased estimations in some deltas with low data quality and small size.

We assess the uncertainty of the time lag using the coefficient of determination (R2) and the statistical significance (P-value) of the (lagged) correlation. In addition, to verify the effectiveness of the analyzed delta-scale lag times, we have recalculated lag times using in-situ measured Qriver with better observational records in five rivers (Brazos, Mississippi, Liaohe, Yellow, and Yangtze) and found identical results (Supplementary Table 2). We perform the sensitivity analyses using alternate delta area polygons that were isotropically dilated/diminished by 5%, respectively (see “Method”). Further, we collected the Qtide and Qwave to characterize the tide- and wave-driven sediment transports in a delta, and defined a dimensionless T-value (Qtide /Qriver) to reflect the relative strength of the riverine and tidal forcings, with higher values representing stronger tidal dominance (Supplementary Table 1).

Results

Changes in fluvial sediment load and delta land area

We find large changes in fluvial sediment supply to deltas between 1990 and 2020. The total annual fluvial sediment load delivered into all studied deltas decreased by 15% from 1990 to 2020 at a rate of 1.38 × 107 t yr?2 (Fig. 1c). Much of this decline occurred before 2010, with the total fluxes lowered by 12% from 3.22 × 109 t yr?1 in 1990–1996 to 2.85 × 109 t yr?1 in 2006–2010 (Fig. 1c and Supplementary Table 3). Individually, over these 31 years, the annual fluvial sediment loads decreased in 36 of the 60 rivers in this study, with a decline of over 20% in 26 rivers (Fig. 1a, b). Among them, four rivers that experienced the greatest declines were all located in Asia, i.e., the Pearl (Zhujiang) River, Liaohe River, Yangtze (Changjiang) River, and Song-Hong (Red) River, with reductions of ?86%, ?85%, ?68%, and ?66%, respectively (Fig. 1a and Supplementary Table 1). In contrast, the annual sediment supply increased in 24 rivers, with increases of over 20% in 16 rivers (Fig. 1a, b). The Burdekin River (Australia), Ural River (Caspian Sea), Zambezi River (Africa), and Nelson River (Canada) showed the highest increased proportion up to 264%, 87%, 83%, and 79%, respectively (Fig. 1a and Supplementary Table 1).

Delta surface area expanded at a rate of 271 km2 yr?1 between 1990 and 2020, albeit with some temporal fluctuations (Fig. 1d). Expressed as a fraction of their total area, delta lands experienced the greatest net gain proportion of 1.98‰ yr?1 between 2001 and 2005 compared to that in 1990–1995 (Supplementary Table 3). Since then, the overall net growth rate of delta land has slowed, especially, it was only 0.03‰ yr?1 between 2006 and 2010, potentially associated with the most dramatic reductions in fluvial sediment inputs (Fig. 1c, d) (Supplementary Table 3). Delta land area change analysis showed that 43 of the 60 deltas grew after 1990, with larger deltas growing faster (Supplementary Fig. 4A). The mega Ganges-Brahmaputra, Amazon, and Mekong deltas gained 83 km2 yr?1, 49 km2 yr?1, and 37 km2 yr?1 between 1990 and 2020, respectively (Supplementary Table 1). The remaining 17 deltas experienced net land loss, with the Mississippi Delta shrinking the fastest at 15 km2 yr?1 (Supplementary Fig. 4B, C). Overall, rates of land gain are strongly tied to annual fluvial sediment supply. There is a significant linear dependency (R = 0.530, P < 0.001) (Supplementary Fig. 4D) that was also found in earlier studies11.

Global-scale response time of deltas

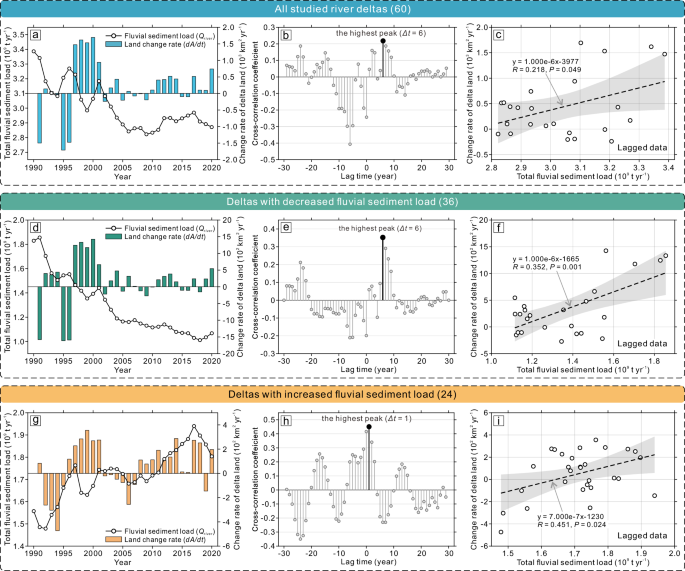
Based on the cross-correlation of the total fluvial sediment supply and changes in delta growth rate for all 60 deltas during the studied periods, we find the highest cross-correlation coefficient of 0.218 at an overall ?t (lag time) of 6 years (Fig. 3a–c). Put differently: global gains and losses in the delta area occurring between 1990 and 2020 seem to reflect fluvial sediment supply changes 6 years prior. Correlation at this time lag is statistically significant (P = 0.049). Furthermore, the lack of correlation at ?t = 0 confirms the findings of previous studies (e.g., Besset et al.19), which were not able to connect sediment input to delta land change at the global scale (Fig. 3c).

Fig. 3: Cross-correlation analyses of fluvial sediment load and delta land area change rates.
figure 3

a Time series of total annual fluvial sediment load and delta land area change rate in all deltas during 1990–2020. b Cross-correlation coefficients of different lag times in 60 deltas with a primary lag time of 6 years. c Linear correlation between the lagged total sediment load and land area change rate in 60 deltas. d–f The time series of annual total fluvial sediment load and land area change rate in 36 deltas with decreased sediment supply, shows cross-correlation analyses with a primary lag time of 1 year, the linear fitting of lagged data is also significant. g–i Time series of total fluvial sediment load and land area change rate in 24 deltas with increased fluvial sediment input, shows cross-correlation analyses with a lag time of 6 years and the linear fitting of lagged data.

Full size image

Restricting our investigation to deltas with a net declining supply over the 31-year period, we also find a lag time of 6 years (Fig. 3d, e). The linear relation of the lagged delta land change rates and fluvial sediment loads here is clearer overall (P = 0.001) (Fig. 3f), and again deviates strongly from the correlation without a time lag. For 24 deltas with increased fluvial sediment supply, the time series generally shows an overall more synchronized growing pattern, most clearly visible from 2002 to 2006 (Fig. 3g). The cross-correlation revealed a lower lag time of only 1 year with a correlation coefficient of 0.451, and the corresponding lagged data of Qriver and dA/dt were also significantly linearly correlated (P = 0.024) (Fig. 3h, i).

Delta-scale differences in lagged response times

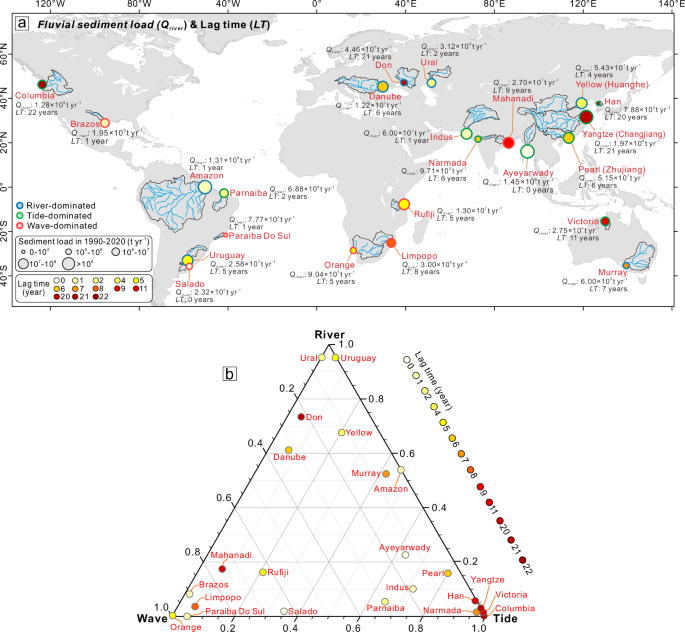
Zooming into the time-series for individual deltas, we find a large variety in sediment supply trends and resulting time lags. The average lag time across all deltas is 2.9 years. However, this average includes some deltas where the lag time is negative (and therefore unphysical) and some are not statistically significant (P > 0.10) (Supplementary Figs. 6–14). For the remaining 23 deltas with positive lag times and P-value of the lagged data ≤ 0.10, we find an average lag time of 6.8 years, similar to the results (i.e., 6 years) when using the globally aggregated data. Lag times varied between 0 and 22 years (Fig. 4a, Supplementary Table 1, and Supplementary Fig. 14).

Fig. 4: Delta-scale lag response timescales.
figure 4

a The global distribution of the 23 classified deltas, shows the annual fluvial sediment load (Qriver) and the studied lag time between 1990 and 2020. b A ternary diagram of 23 deltas with different relative river, tidal, and wave forcings, the corresponding color of the solid circle represents lag time in this study.

Full size image

Lag times seem to be partially controlled by delta morphology, as determined by the relative strengths of Qriver, Qtide, and Qwave (driven sediment fluxes at the river mouth) (see ‘Methods’, Supplementary Table 1). Four of the five deltas with the longest lag times are all tide-dominated ones (Supplementary Fig. 11B, C). Tide-dominated deltas also have the overall longest average lag time of 9.9 years. The river-dominated and wave-dominated deltas respond faster to fluvial sediment supply changes, after 6.6 and 4.1 years, respectively (Fig. 4a and Supplementary Fig. 11C).

The effect of morphology on the response time is also visible in the ternary diagram (Fig. 4b). Most river deltas with shorter lag times (except for the Don Delta) were sparsely distributed at the end with the stronger river forcing (Qriver), such as the Ural, Uruguay, and Yellow deltas (Fig. 4b). Toward the tide-dominated corner, however, deltas with longer response times (the redder background) clustered more closely (Fig. 4b). Especially the Columbia and Yangtze deltas, which are subject to strong tidal dominance (Qtide) and hold the longest lagged times in all studied deltas between 1990 and 2020, up to 22 and 21 years, respectively (Supplementary Table 1 and Supplementary Fig. 11C). Meanwhile, in the Ayeyarwady and Indus deltas, farther away from the strongest tide-dominated end, the lag time shortens rapidly compared to the two above deltas, indicating that their deltaic lands respond more directly to fluvial sediment supply changes between 1990 and 2020. In addition, in the deltas under stronger wave forcing (Qwave), the lag times were somewhat more variable, which suggests the geomorphic response behaviors were more complex, and they were weakly related to fluctuations in the fluvial sediment supply (Fig. 4b).

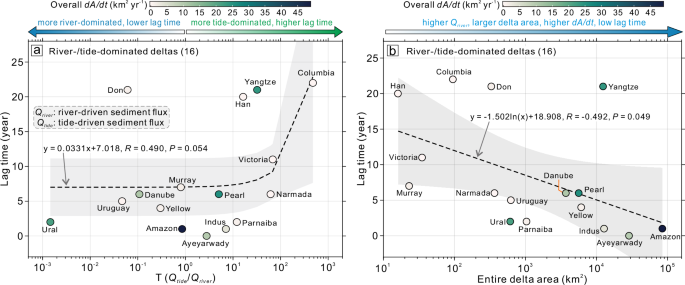
The differentiation between river-dominated and tide-dominated deltas shows that tidal dominance (the relative strength of tidal current over fluvial currents at the river mouth) can increase the lag time (Fig. 5a, see “Methods”). Particularly, the Colombian and Ural deltas (non-open water in the Caspian Sea) had the highest and lowest T-values (Qtide/Qriver) of 478.1 and 0.001, respectively, thus corresponding to a lag time of 22 and 2 years (Fig. 5a and Supplementary Table 1). In addition to the effect of tidal dominance, we also find an effect of delta size on the lag time. The large river deltas seem to respond more rapidly to changes in the fluvial sediment flux (Fig. 5b). This is perhaps counterintuitive. For a given fluvial diffusivity42, one would expect the response time to scale with the delta surface area. However, we find that larger deltas, such as in the Amazon, Ayeyarwady, Indus, and Yellow Deltas, have a short time lag. A possible reason for this is that the larger sediment loads of the larger deltas, result in bigger signals at the coast that are therefore easier to detect in the Landsat satellite imagery.

Fig. 5: Lag times and the relative fluvial-marine forcings in deltas.
figure 5

a The relationship between the T-value (the ratio of river and tidal forcings) and lag time in 16 river-/tide-dominated river deltas, shows an overall significant positive linear fitting trend. b The relationship between the entire delta area and lag time in 16 river-/tide-dominated river deltas indicates that a larger delta responds faster to changes in annual fluvial sediment load between 1990 and 2020.

Full size image

Discussion

Based on globally aggregated data, we found that the reduction in fluvial sediment supply triggered a 6-year lag in the slowdown of the overall delta surface area growth rate between 1990 and 2020. However, delay effects were highly variable, and more difficult to detect for individual deltas due to data availability and accuracy.

Earlier studies on time lags found much higher lags, though in different systems such as barrier islands22,43,44,45,46. These longer lags might have appeared because the changes in forcing were subtle compared to the fluvial sediment supply (e.g., sea-level rise acceleration). It may also be possible that longer records (beyond the 31 years of our time series here) will expose evidence for longer time lags. Similarly, the reason that other studies (e.g., Edmonds et al.47) did not need to include a time lag may be because of the limited time resolution of the data. Time lags of ~1–10 years might be hidden from sparsely sampled decadal data.

There is likely an effect of grain size on deltaic lag times. Fine-grained sediments do not necessarily facilitate land area gain; much of it may be either transported seaward or increase delta plain vertical aggradation48,49,50,51, both leading to longer time lags before delta land area change becomes visible. A recent study found that sediment turbidity along deltaic coasts did not decline overall in response to the reduced fluvial sediment supply20. Delta land growth was also uncoupled from turbidity; such asynchrony may be caused by lagged responses11,20,52,53.

We found a difference in lag time between deltas where fluvial sediment increased vs. decreased, with decreases in upstream sediment supply taking a longer time to manifest themselves in delta land changes (Fig. 3d–f). The difference in delta response can be because of eco-geomorphic feedbacks that vary between wetland establishment, erosion, and succession54,55,56. It can also be because of bed armouring or other types of sedimentological effects. Along the Ebro River (Spain), for example, armour layers have established downstream of dams, during high flows some medium grain-size bed sediments are eroded, thereby increasing the total sediment transport; such compensation of riverbed sediment resulted in a delayed response of total fluvial sediment declines toward the delta, potentially on the order of centuries57. A faster response to sediment increase is shown for the Elwha. After the removal of Glines Canyon and Elwha dams on the lower Elwha River (UAS) in 2012, up to 30 Mt of riverbed sediment were released and transported downstream. Delta sedimentation rates increased primarily from coarse-grained sedimentation, and related land growth rates peaked 1–2 years later27,58.

Deltas with strong tidal dominance have longer response times. Some studies have indicated that stronger tide forcing (larger Qtide) can largely control hydrodynamics and sediment transports within the funnel-shaped deltaic channels and tidal flats, due to the amplification effect and intensive mixing processes, thereby influencing delta land growth patterns and rates along with Qriver49,59,60,61. Numerical simulations and experimental results have demonstrated that tidally dominated bi-directional flows with high turbidity and pumping effects can increase overall sediment accumulation rates within a delta complex when subject to changing external drivers39,62,63. In addition, the high-roughness and bifurcated deltaic channel-shoal configuration can greatly attenuate hydrodynamic energy and sediment erosion, thereby enhancing the geomorphic stability and constraining the overall distributary mobilities at the landscape scales49,61,64,65.

In our study, the five deltas (i.e., the Columbia, Victoria, Narmada, Yangtze, and Han) with the strongest tidal dominance (the higher T-value, Qtide/Qriver) all exhibited longer lagged times (≥ 6 years) (Fig. 5a). Moreover, in these deltas with lower Qriver, the relative tidal dominance increases coupled with accelerated SLR, which will re-transport marine-sourced sediments landward to feed delta land growth under reducing fluvial sediment supply (Qriver), and thus increase response time and disturb the \(\frac{{{{\rm{dA}}}}}{{{{\rm{dt}}}}}\,\propto \,{Q}_{{river}}\) relationship66,67,68. For instance, in the tide-dominated Yangtze Delta, the annual fluvial sediment load has decreased by over 70% over the last five decades after damming and sand mining52,69. A time lag of declining turbidity at the coast was found of approximately 12 years70. Yet, the extensive salt marshes, tidal flats, and shoals continue to advance seaward, in this case partially facilitated by marine sediment inputs from the delta front under enhancing tidal dominance, especially after the implementation of the mega Three Gorges Dam in 200332,53,71,72.

Many wave-dominated deltas did not show significant time lag, and only 7 of the 22 wave-dominated deltas in this study met the criteria (lag time ≥ 0 and P-value of lagged data ≤ 0.10) (Fig. 4b and Supplementary Fig. 11). This is likely due to their relatively small size and the local stronger wave power. The typical model for wave-dominated deltas suggests that they grow from the divergence of alongshore sediment transport, which is mostly coarse grained73,74,75,76. Therefore, most of the fine-grained sediment does not directly lead to land growth, and the medium-/coarse-grained fraction of Qriver is primarily associated with land changes in river deltas; however, the Qriver captured by Dethier et al.7 includes a significant fine-grained fraction7. In addition, the coarse-grained fraction would likely have a longer delay time in the upstream fluvial domain26,77. The above reasons may explain why wave-driven delta dynamics will likely cause delta land growth rates to deviate from the study hypothesis of \(\frac{{{{\rm{dA}}}}}{{{{\rm{dt}}}}}\,\propto \,{Q}_{{river}}\) relationship.

Moreover, sediment retention in delta plain is also highly variable, which will also affect delta response lag times2,39,56. Deltas that retain a large fraction of their supply could act as a buffer, such that delta land changes do not respond immediately to the short-term fluctuations in fluvial sediment supply40. For example, the long time lag of 21 years in the Yangtze Delta may have been caused by extensive tidal wetlands and mouth bars32,52,53,72 (Supplementary Figs. 11, 15 and 16 and Supplementary Table 1). Similarly, sheltered by sand spits on either side in the Columbia Delta, fluvial sediment trapping is more efficient in the low-lying shoals and salt marshes, thus, we detected a longer lag time of up to 22 years (Supplementary Figs. 15 and 16)78. In contrast, in the Ayeyarwady and Indus deltas, strong prevailing winds, waves, and alongshore currents exacerbate coastal land erosion and net sediment loss, thereby forming smoothed and coarse-grained sandy beaches, even though some of the riverine sediment inputs can accumulate within the inner delta channels and wetlands (Supplementary Figs. 15 and 16)79,80. Such low sediment retention efficiencies could have enabled the land area changes in both deltas to respond rapidly to fluctuations in upstream sediment supply, lagging 0 and 1 year, respectively (Supplementary Table 1).

There is uncertainty in the estimates of time lags. First, the annual fluvial sediment load used was obtained from Dethier et al.7 Their Landsat-obtained surface sediment flux trends might differ from those further down in the water column, especially in some river reaches with strong (tidal) circulation. Second, gaps in the original monthly flow discharges were filled with different time-running windows to generate time series of the discharge, which may be limited by low data availability7. Third, most downstream hydrologic monitoring stations are still some distance away from the delta, in these areas, this study partly scaled the flow discharge by watershed area to compensate for underestimation. Therefore, there remains a large gap in fully developing an evaluation of the replenishment of suspended/bed sediment along the downstream reaches and tidal rivers2,69,81,82. Despite these uncertainties, a comparison of time lag calculations using in-situ data gave identical results (Supplementary Figs. 12 and 13 and Supplementary Table 2). Concerning delta area change, these data are limited by satellite revisit periods, cloud cover, cloud shadows, and spatial resolution of Landsat satellite observations, leading to possible errors and underestimates/overestimates at the individual delta scale11,34,83,84. These offsets/errors may pose some uncertainties for lagged responses and time scales between Qriver and dA/dt in individual deltas in our study, which may lead to negative lag times (15 of 60 deltas) and weak correlations (Supplementary Fig. 11 and Supplementary Table 1).

In addition, human activities on deltas and adjacent coastal areas may also create uncertainty. Human activities on delta plains affect delta land growth through, for example, reclamation, channelization, dykes, and dredging15,47,53,69,85,86. For instance, large-scale reclamations have been implemented in the Yangtze Delta, which contributed to an overall rapid net increase of delta land by 24 km2 yr?1 between 1990 and 2020 (Supplementary Table 1). These direct human effects on deltas are difficult to separate from natural delta land change mechanisms.

Furthermore, herein, we used the globally aggregated fluvial sediment load and land change rates in 60 deltas, then calculated an overall lag time of 6 years on a global scale, which may slightly differ from the average lag time (2.9 years) of all individual river deltas. However, this method can avoid to some extent the errors arising from delta-scale uncertainties, including low remote sensing-based detectability and negative lag time (unphysical) in some deltas. Even so, both lag times for all studied deltas keep a similar order of magnitude, indicating the high vulnerability of delta land to the lowering fluvial sediment supply.

Findings here could inform delta adaptive strategies for coping with ongoing multiple risks. Globally, the delta land growth rate slowdown between 1990 and 2020 lagged the reduction in upstream sediment supply by 6 years. However, there is great variability between river deltas, and for many deltas, we were not able to find a significant relation between fluvial sediment supply change and land area change, despite our 31-year records. Such asynchronous responses and lag time scales will affect ecological restoration and adaptation to disaster defense in vulnerable deltaic wetlands4,8,46,56,87,88. If the effect of dam construction on delta land change is unclear, then the result of dam removal will be as well. The longer time lags in tide-dominated deltas also make it challenging to predict future change and pinpoint causal factors in a deltaic system11,62,88. Our findings highlight the complicated relation between fluvial sediment supply and delta land growth, with short timescale adjustments affected by internal dynamics.

Methods

Obtaining fluvial sediment loads

Fluvial suspended sediment load data used here were publicly obtained from Dethier et al.7 This dataset estimated monthly sediment loads for over 400 rivers worldwide based on Landsat satellite imagery and measured water discharges. From the 400 rivers, we selected 60 deltas where the land surface area data were also available (see “Method” 4.3). Satellite-based estimated annual sediment load (Qriver) in this dataset showed high global consistency with in-situ measured records; the potential errors are not systematic7. For instance, in three mega rivers with well-observed records, i.e., the Mississippi, Yangtze, and Pearl Rivers, the overall differences in cumulative Qriver in 1984–2020 were 6%, 4%, and 11%, respectively. Therefore, the estimated Qriver can provide important insights into the geophysical changes of modern river deltas. We thus converted the monthly time series to a yearly time series, and used a robust linear regression with a 5-year window to remove outliers. Tests with other smoothing windows did not significantly affect the results presented in this study.

Define the boundary polygons for river deltas

We defined the specific boundary polygons for 60 deltas to quantify the delta surface areas and growth rate changes between 1990 and 2020. Depending on our study objectives and data availabilities, the given boundaries were variable in the literature. Therefore, we synthesized the hypotheses and the JRC Yearly Water Classification History dataset34, and followed the below approaches to draw boundary polygons for each delta in Google Earth Pro. Two typical examples of the Zambian and Limpopo deltas here were illustrated to indicate polygon definitions of fluvial-tidal-dominated and wave-dominated deltas, respectively (Supplementary Fig. 3). In general, the delta polygon was delimited by an upstream beginning transect and two progressively extending boundaries on either side, with the seaward boundary sufficiently encompassing all active delta surface area and parts of offshore areas (Supplementary Fig. 3). Moreover, such an approach also considered the own geomorphic configurations, geographical conditions, and literature in deltas.

First, the upstream beginning transect was located in a relatively straight channel that gradually widened downstream, which was less disturbed by human activities and covered the extent of possible channel migration extent since the 1980s, such as in the deltaic apex. Thus allowing most of the downstream bifurcation nodes and distributives to be in the defined polygon. If in a bifurcated and strongly anthropogenically disturbed delta, some agriculture or farming activities were developed in the subaerial lands (e.g., the mega-Mekong Delta), these deltaic portions were partially avoided since they remained relatively stable and also classified as unobserved areas in JRC Yearly Water Classification History dataset during the study period34. Second, two progressive boundary lines were drawn to ensure the outermost bifurcated channels were encompassed. The landward polygon covered the extent of channel migrations since the 1980s. Besides, two points of intersection with shorelines should be positioned at the maximum extent for active land building in a delta. In particular, if the outermost channel in a bifurcated delta bordered the mainstream or one tributary of another delta, the centerline of the two deltas was defined as the lateral boundary on that side. Third, the seaward boundary was kept away from delta surface lands to allow all coastal active areas to be covered, such as tidal wetlands and part-time exposed tidal shoals, and maintained as much as possible in a regular shape with multiple points. The uncertainty was assessed by expanding and shrinking the delta polygons by 5%, which did not significantly affect the resulting lag time (Supplementary Fig. 5). The cross-correlations were 0.222 and 0.231, respectively, both with a lag time of 6 years, which were the same as that of \({{Area}}_{100\%}\) (Fig. 3 and Supplementary Fig. 5). P-values of the linear fitting of lagged data of sensitivity testing were below 0.10. Therefore, the consistent lag times and similar correlation coefficients showed the overall efficiency of defined delta polygons.

Calculations of delta land areas and growth rate changes

The drawn and finalized shapefiles of delta polygons were uploaded to Assets of the Google Earth Engine platform, then they can be used to retrieve the classified areas from the Yearly Water Classification History dataset (v1.4)34. Based on satellite-sensed techniques, this dataset inverted and recorded changes in yearly water regimes on the earth’s surface since 1984. Specifically, land features were classified into not waters, seasonal, permanent waters, and the unobserved areas that remained relatively stable over the period were also indicated. Hence, in this study, the extent of non-waters and seasonal waters retrieved within each delta polygon, which were defined as the active delta surface area, and summed both values to obtain the total delta land area. After examining the results and change tendencies of the land area in each delta, there were some missing values and outliers due to the low availability of Landsat satellite imagery, which was influenced by the revisit period of satellite observations, spatial resolutions, and weather conditions11,34. Hence, the ‘movmean’ and ‘rlowess’ methods in MATLAB were used, respectively, to fill in missing values and remove the outliers. These processes were tested several times to achieve data that were as reasonable and effective as possible.

Limited by satellite observations, a total of 60 worldwide river deltas were selected to analyze their response behaviors and potential lag times. Time series of fluvial sediment supply and surface area in each delta were obtained between 1990 and 2020. The annual fluvial sediment loads and overall land growth rates in 60 deltas over the past 31 years were presented in Supplementary Table 1.

Analyzing lagged response times using the cross-correlation method

The cross-correlation method can quantify the primary lag time of different variables by calculating the correlation of shifted data with varying time steps. It has been commonly used in numerous relevant studies of geosciences and environmental sciences and showing strong applicability and rationality35,36,37. Herein, for two time series of \({{Q}_{{river}}}_{i}\) and \({\frac{{dA}}{{dt}}}_{j}\) between 1990 and 2020 (Fig. 2b), the correlation coefficients between the former and the gradually lagged latter by time t can be calculated (Eqs. 1–3), which is the ratio of the covariance to the root-mean-square variance. Then, the primary lagged response time (?t) can be determined by the highest peak of the correlation coefficient (Fig. 2c).

$${{{\rho }}}_{{{i}},{{j}}}=\frac{{{{\gamma }}}_{{{i}},{{j}}}}{\sqrt{{{{\sigma }}}_{{{i}}}^{2}{{{\sigma }}}_{{{j}}}^{2}}}$$
(1)
$${\hat{\gamma }}_{i,j}=\frac{1}{{{{\rm{N}}}}}{\sum }_{t=1}^{{{{\rm{N}}}}}\left[\left({{Q}_{{river}}}_{i}^{t}-{\overline{{Q}_{{river}}}}_{i}\right)\left({\frac{{dA}}{{dt}}}_{j}^{t}-{\overline{\frac{{dA}}{{dt}}}}_{j}\right)\right]$$
(2)
$${\hat{\rho }}_{i,j}=\frac{{\sum }_{t=1}^{{{{\rm{N}}}}}\left[\left({{Q}_{{river}}}_{i}^{t}-{\overline{{Q}_{{river}}}}_{i}\right)\left({\frac{{dA}}{{dt}}}_{j}^{t}-{\overline{\frac{{dA}}{{dt}}}}_{j}\right)\right]}{\sqrt{{\sum }_{t=1}^{{{{\rm{N}}}}}{\left({{Q}_{{river}}}_{i}-{\overline{{Q}_{{river}}}}_{i}\right)}^{2}{\sum }_{t=1}^{{{{\rm{N}}}}}{\left({\frac{{dA}}{{dt}}}_{j}-{\overline{\frac{{dA}}{{dt}}}}_{j}\right)}^{2}}}$$
(3)

where\(\,{{Q}_{{river}}}_{i}\) and \({\frac{{dA}}{{dt}}}_{j}\) are time series of two variables,\(\,{\overline{{Q}_{{river}}}}_{i}\) and \({\overline{\frac{{dA}}{{dt}}}}_{j}\) are the mean of the two, t (0, ±1, ±2, ….) is the delay time, and \({\hat{\rho }}_{i,j}\) is the cross-correlation coefficient with values between ?1.0 and 1.0.

First, the lag time of all 60 deltas in response to the total fluvial sediment supply was analyzed, showing the highest peak of cross-correlation coefficient was 0.218 at a lag of 6 years (Fig. 3a–c). Second, there were 36 and 24 deltas, respectively, showing reductions and increases in sediment inputs during the past 31 years, with lagged response times of 6 and 1 year for delta land area changes (Fig. 3d–i). In this paper, we chose the unbiased cross-correlation coefficient to show in the linear correlation of lagged data because it is more conservative (Fig. 3). Third, the lag time of individual river delta and corresponding linear correlation of lagged sediment load and land area change rate were also calculated (Supplementary Figs. 6–13). There was a total of 23 deltas with significance test P-value less than 0.10 in the linear fitting of the lagged data and positive lag times were selected in this study (Supplementary Figs. 11 and 14). Therefore, the above results in 23 selected deltas were used to analyze the possible linkages between lag times and fluvial sediment loads and terrestrial-marine hydrodynamic conditions at the delta scale.

River-, tide-, and wave-driven sediment fluxes and T-value (Q tide /Q river) definition

The mean sediment fluxes driven by river, tide, and wave in each delta were obtained to characterize the relative strengths of three hydro-forcings. First, river-driven sediment flux (Qriver) was the mean of fluvial input between 1990 and 2020 in this paper. Second, tide- and wave-driven sediment flux (Qtide and Qwave) were obtained from Nienhuis et al.11 The Qtide was estimated based on the dominant tidal amplitude, tidal period, channel slope, and channel width-to-depth ratio in a delta. Qwave was derived by calculating the maximum potential alongshore sediment transport driven by waves with different approach angles.

Here, a total of 23 specified individual deltas (P-values below 0.10 in the linear fitting of lagged data) with lag times (≥ 0) were projected onto a ternary diagram determined by the river-, tide-, and wave-driven sediment fluxes (Fig. 4b). The concentration and properties of these deltas at different ends in such diagram were analyzed to indicate the different effects of hydro-dominances. Moreover, considering the study hypotheses and objectives, a T-value (Qtide/Qriver) characterizing the relative strength of tidal and riverine dynamics was constructed. The larger T-value represents the stronger tidal dominance. Results showed that in the 23 deltas selected above, the highest T-value reached 478.136 in the Columbia Delta (North America), and the lowest T was only 0.0002 in the Ural Delta (Caspian Sea). More information on river-, tide-, wave-driven sediment fluxes and the T-values in all studied deltas were documented in Supplementary Table 1.